Zenone e i Paradossi

Zenone fu allievo di Parmenide, entrambi considerati come gli esponenti di spicco della scuola di pensiero eleatica. Egli visse ad Elea, qui nacque nel 489 a.C., e cadde per cospirazione contro un tiranno nel 431.

Parmenide fu accusato di essere portatore di una logica negatrice della realtà, che andasse contro il senso comune. Zenone fece così della sua filosofia una prova delle dottrine del maestro. Polemizzò con i suoi contemporanei (ad esempio i Pitagorici), l’assurdità di alcune tesi che avessero come basi i principi della molteplicità e del movimento.

I Paradossi di Zenone

Come detto Zenone si impegnò nella difesa del suo maestro. E lo fece attraverso i famosi “argomenti”; o meglio paradossi che ponevano le radici sul movimento e l’infinita molteplicità e divisibilità dello spazio e del tempo. Muovendosi così i passi per una dimostrazione per assurdo. Gli argomenti proposti da Zenone ne furono quattro.

Primo e Secondo Argomento

Primo Argomento.

Un mobile che va dal punto A al punto B deve prima toccare il punto C, posto a metà del percorso A-B, e ancor prima il punto D, posto a metà del percorso A-C, e così via all’infinito. Ma è impossibile in un tempo finito percorrere uno spazio infinito, dunque il mobile non percorrerà mai lo spazio A-B.

Secondo Argomento: “Achille piè veloce” o Achille e la Tartaruga

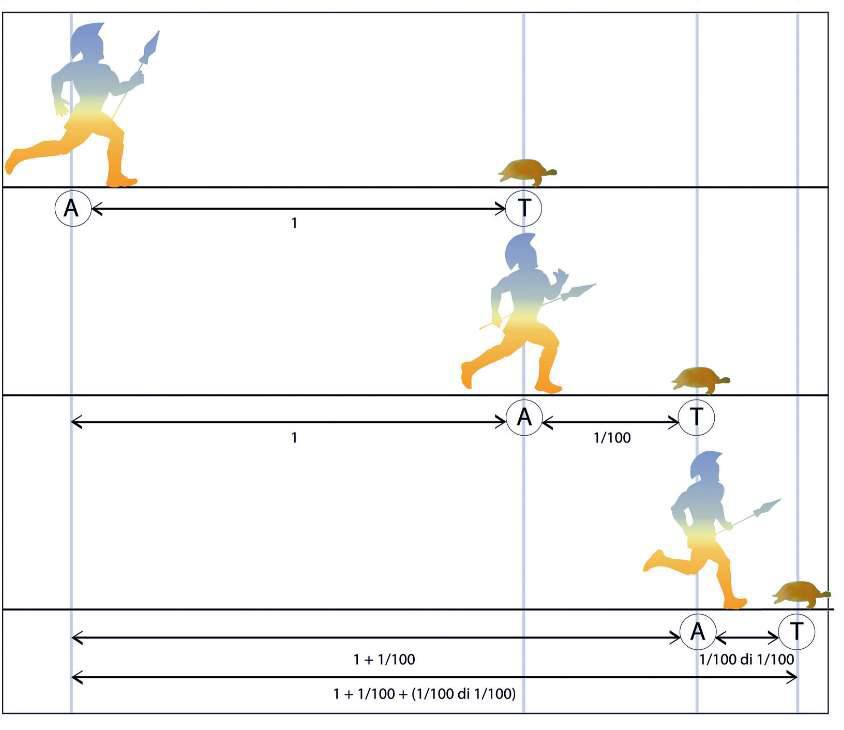
Achille “piè veloce” non raggiungerà mai la lenta tartaruga se questa parte da un punto B più avanzato del punto A da cui parte Achille. Quando infatti Achille raggiungerà B, la tartaruga sarà in C e quando Achille sarà in C la tartaruga sarà in D. La distanza tra le loro posizioni sarà sempre più piccola, ma non potrà annullarsi mai.

Come è ben evidente dai primi due argomenti, Zenone parte dal fatto che lo spazio è infinitamente divisibile. Tali argomentazioni prendono una piega matematica. In particolare nel famoso argomento di Achille, come evidenziato nell’immagine soprastante. Nel primo argomento infatti un mobile non potrà mai raggiungere la sua meta, a causa dell’infinità dello spazio. Nel secondo Achille non raggiungerà mai la tartaruga, pure se è più veloce. Si avvicinerà, ma ci sarà sempre, infinitamente, una distanza che li separa. Evidente è qui la sfasatura tra due piani, quello logico-matematico e quello reale.

Terzo e Quarto Argomento

Terzo Argomento.

Una freccia che per ipotesi sia in movimento, essendo in ogni singolo istante del tempo in uno spazio uguale alle sue dimensioni, sarà in quiete.

Il presupposto di questo argomento è l’inverso di quello di Achille. Zenone infatti considera il preciso momento di un istante di tempo, ponendo tale divisibilità del tempo. In quelle condizioni il movimento della freccia non c’è, essa pare immobile.

Quarto Argomento.

Rispetto a un punto fermo A, due oggetti situati in punti opposti di uno stadio e che poi si muovono alla stessa velocità, in senso contrario tra loro, percorrono uno spazio che è nello stesso tempo uguale (rispetto al punto A) e doppio (rispetto all’altro oggetto in movimento).

Tale paradosso di Zenone viene definito come quello delle “masse dello stadio“. La sua comprensione non è di immediata facilità, ma pone le sue basi ancora in fondamenti matematici. Il paradosso è che qui, un oggetto ha una velocità sia pari alla metà che al doppio della stessa. Questa velocità cambia in base al parametro tenuto da riferimento. Ed è chiaro che sarà doppia rispetto ad un altro oggetto, che ugualmente si muove verso l’altro. Invece considerando il punto immobile, centrale ai due, la velocità sarà la metà di quella considerata precedentemente.

Considerazioni finali

Alla conclusione dell’esposizione dei famosi argomenti di Zenone, vediamo di chiarirci un po le idee sul filosofo. Ciò che l’allievo di Parmenide voleva dimostrare, non era certamente l’impossibilità del movimento. Sarebbe irrazionale promuovere certe posizioni. Eppure era il solo modo per liberare il maestro da opposte, ma altrettanto irrazionali, accuse di immobilismo.

I due piani, quello reale e quello del pensiero sono difficilmente legabili in modo rigoroso. Una difficoltà non solo logica, ma pienamente filosofica. Ed anche per questo, che alcuni argomenti di Zenone, rimangono ancora oggi inconfutabili!